Proof-oriented Programming in F*

Nik Swamy

Microsoft Research

Goldman Sachs Seminar, March 10, 2021

Towards High-assurance Software

Through Code Analysis (1)

CompilerWarnings

Through Code Analysis (2)

StaticAnalysis

Through Code Analysis (3)

StateSpaceExploration

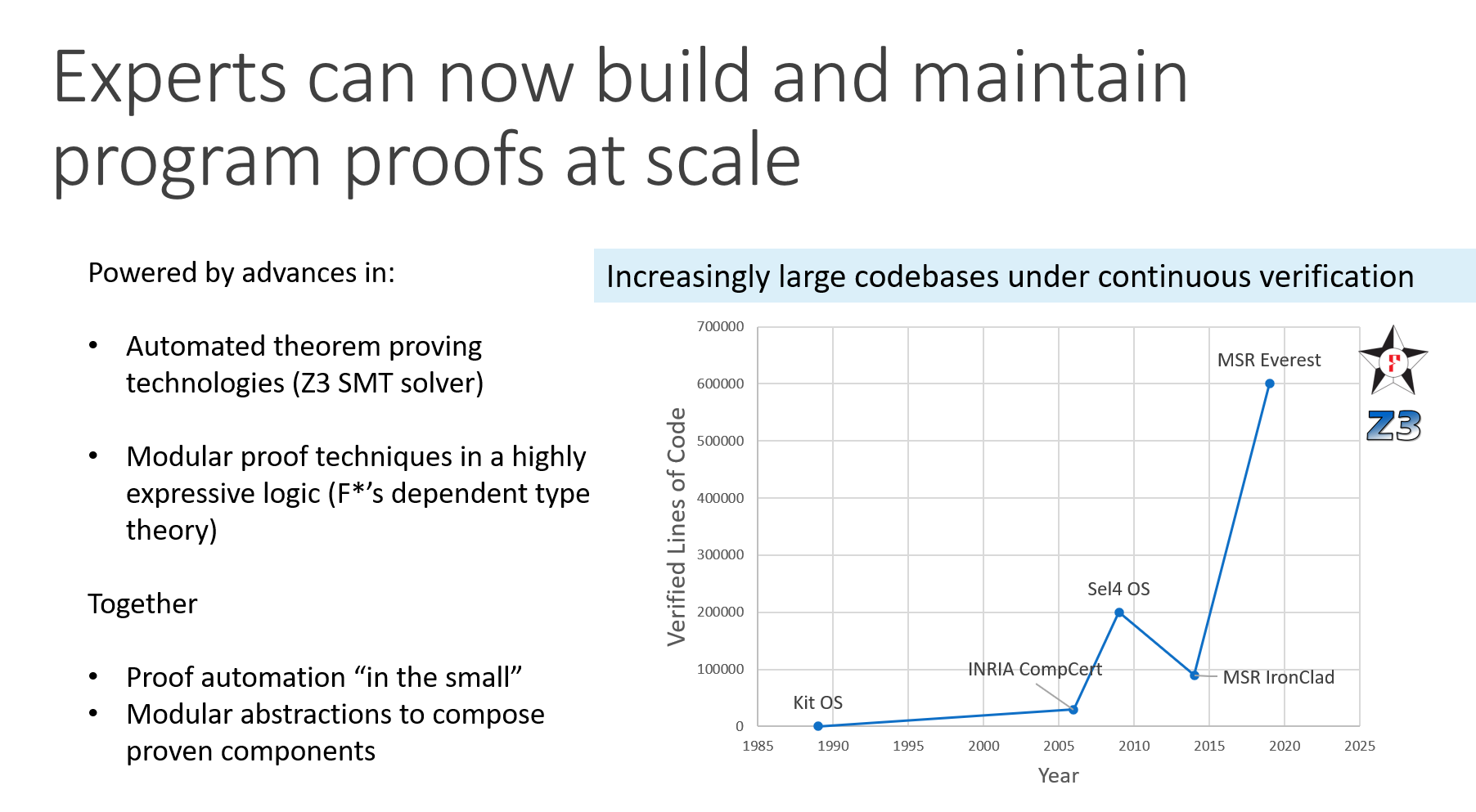
Full-scale Program Proofs

Mathematical specifications of correctness and security
Machine-checked proof that the code does not deviate from the spec
Foundational: Against a formal machine model
Integrated: Single theorem covering all the code

Scale

What is F*?

Functional programming language with effects
- like OCaml, F#, Haskell, …
- F* extracted to OCaml or F# by default
- Subset of F* compiled to efficient C code and to Wasm
Semi-automated program verifier using automated theorem proving
- like Dafny, FramaC, Why3, …
With an expressive core language based on dependent type theory
- like Coq, Lean, Agda, Idris, …
A metaprogramming and tactic framework for interactive proof and user-defined automation
- like Coq, Isabelle, Lean, PVS, etc.
And many foundational program logics for embedded DSLs
- Many variants of Hoare logic for sequential programs
- Concurrent separation logic, for concurrent and distributed programs
- Relational Hoare logic, for program equivalence and security proofs

A first taste

Write code in a syntax similar to OCaml, F#, Standard ML:

let rec factorial n =
  if n = 0 then 1
  else n * factorial (n - 1)

Give it a specification, claiming that factorial is a total function from non-negative to positive integers.
```
val factorial: n:int{n >= 0} -> Tot (i:int{i >= 1})
```

Ask F* to check it

fstar factorial.fst
Verified module: Factorial
All verification conditions discharged successfully

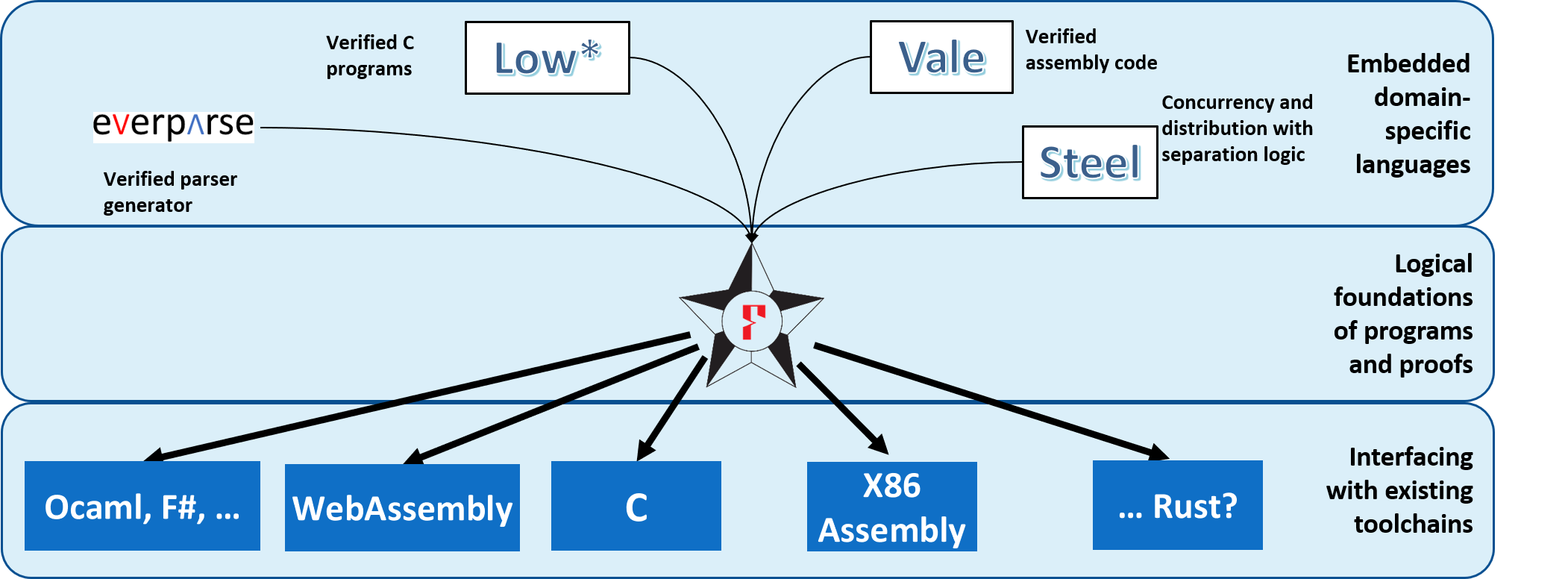
The F* Landscape

FStar-Arch

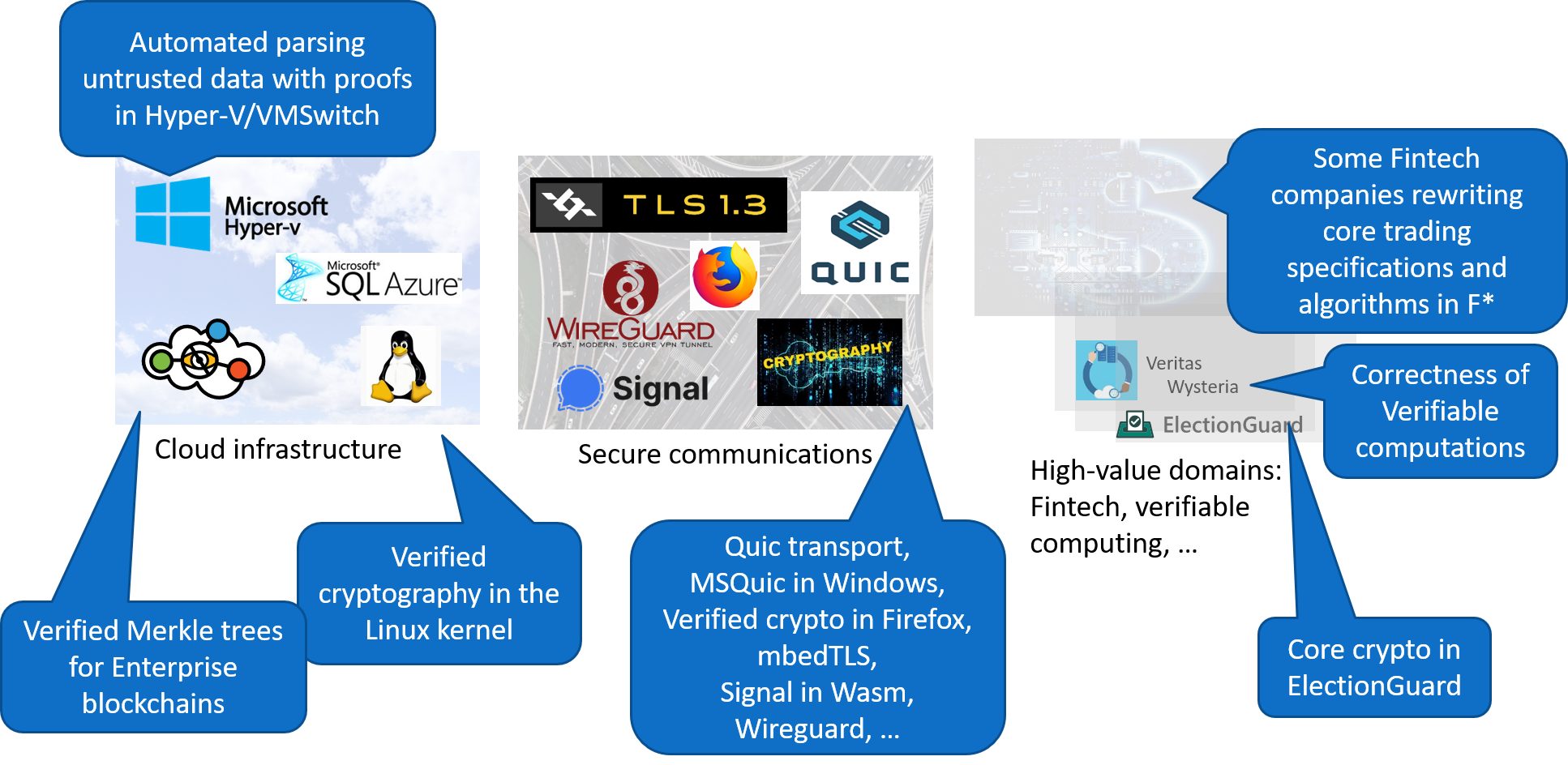
Program Proofs in F* for Billions of Unsuspecting Users

Billions

Contributors

Microsoft Research, Inria Paris, CMU, MIT, Rosario, …

many former members, interns, external contributors, … you?

The rest of this lecture

Today

The functional core of F*
Several style of proof illustrated on simple functional programs
Encoding effects: Simple verified stateful programming
Advanced stuff: A taste of what is possible

Basic types

Informal mental model: Types as sets of values
The empty type: It has no values
```
type empty =
```
The singleton: It has exactly 1 value
```
type unit = ()
```
Boolean: It has exactly 2 values
```
type bool = true | false
```
…

The functional core of F*

Recursive functions

let rec factorial (n:int) : int =
    if n = 0 then 1 else n * (factorial (n - 1))

Inductive datatypes (immutable) and pattern matching

type list (a:Type) =
  | []     (* Nil  *) : list a
  | _ :: _ (* Cons *) : hd:a -> tl:list a -> list a

let rec map (f: a -> b) (x:list a) : list b =
  match x with
  | [] -> []
  | hd :: tl -> f hd :: map f tl

Lambdas (unnamed, first-class functions)

map (fun x -> x + 42) [1;2;3] ~> [43;44;45]

type nat = x:int{x>=0}

Informal mental model: A type describes a set of values

let empty = x:int { false } //one type for the empty set
let zero = x:int{ x = 0 } //the type containing one element `0`
let pos = x:int { x > 0 } //the positive numbers
let neg = x:int { x < 0 } //the negative numbers
let even = x:int { x % 2 = 0 } //the even numbers
let odd = x:int { x % 2 = 1 } //the odd numbers
let prime = x:nat { forall n. x % n = 0 ==> n = 1 || n = x } //prime numbers

Refinements introduced by type annotations (code unchanged)

let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1))

Logical obligations discharged by SMT (simplified)

n >= 0, n <> 0 |= n - 1 >= 0
n >= 0, n <> 0, factorial (n - 1) >= 0 |= n * (factorial (n - 1)) >= 0

Refinements eliminated by subtyping: nat<:int

let i : int = factorial 42
let f : x:nat{x>0} -> int = factorial

Dependent types

Dependent function types (), here together with refinements:
```
val incr : x:int -> y:int{x < y}
let incr x = x + 1
```
Can express pre- and post- conditions of pure functions
```
val incr : x:int -> y:int{y = x + 1}
```
Exercise: Can you find other types for incr?

Total functions in F*

The F* functions we saw so far were all total

Tot effect (default) = no side-effects, terminates on all inputs

val factorial : nat -> Tot nat
let rec factorial n = (if n = 0 then 1 else n * (factorial (n - 1)))

Quiz: How about giving this weak type to factorial?
```
val factorial : int -> Tot int
```

  let rec factorial n = (if n = 0 then 1 else n * (factorial (n - 1)))
                                                              ^^^^^
  Subtyping check failed; expected type (x:int{x << n}); got type int

factorial (-1) loops! (int type in F* is unbounded)

Semantic termination checking

based on well-founded ordering on expressions (<<)
- naturals related by < (negative integers unrelated)
- inductives related by subterm ordering
- lex tuples %[a;b;c] with lexicographic ordering
order constraints discharged by the SMT solver

arbitrary total expression as decreases metric

val ackermann: m:nat -> n:nat -> Tot nat (decreases %[m;n])
let rec ackermann m n =
  if m=0 then n + 1
  else if n = 0 then ackermann (m - 1) 1
  else ackermann (m - 1) (ackermann m (n - 1))

default metric is lex ordering of all (non-function) args
```
val ackermann: m:nat -> n:nat -> Tot nat
```

Types are specifications; Total functions are proofs; Recursion is induction

let rec length (xs:list a) : nat =
  match xs with
  | [] -> 0
  | _::tl -> 1 + length tl

let rec append (xs ys : list a) : list a =
  match xs with
  | [] -> ys
  | x :: xs' -> x :: append xs' ys

Prove that the length of append is the sum of the lengths of its arguments
```
let rec append_length (xs ys : list a) : Lemma (length (append xs ys) = length xs + length ys)
    = match xs with
      | [] -> ()
      | x :: xs' -> append_length xs' ys
```
- Proof by induction on xs
  - Base case, xs=[] is easy: append [] ys = ys /\ length [] = 0
  - Step: Use IH by calling function recursively on smaller arguments
  - Sugar: Lemma p = u:unit { p } `

More Lemmas

let snoc l h = l @ [h]

let rec reverse (l:list a) : list a =
  match l with
  | [] -> []
  | hd::tl -> snoc (reverse tl) hd

let rec rev_snoc (l:list a) (h:a)
  : Lemma (reverse (snoc l h) == h::reverse l)
  = match l with
    | [] -> ()
    | hd::tl -> rev_snoc tl h

let rec rev_involutive (l:list a)
  : Lemma (reverse (reverse l) == l)
  = match l with
    | [] -> ()
    | hd::tl -> rev_involutive tl; rev_snoc (reverse tl) hd

Proof of a program: QUICKSORT

let rec quicksort (f:total_order a) (l:list a)
  : Tot (m:list a{sorted f m /\ is_permutation l m})
        (decreases (length l))
  = match l with
    | [] -> []
    | pivot::tl ->
      let hi, lo = partition (f pivot) tl in
      let m = quicksort f lo @ pivot :: quicksort f hi in
      permutation_app_lemma pivot tl (quicksort f lo) (quicksort f hi);
      m

let permutation_app_lemma (hd:a) (tl:list a)
                          (l1:list a) (l2:list a)
   : Lemma (requires (is_permutation tl (l1 @ l2)))
           (ensures (is_permutation (hd::tl) (l1 @ (hd::l2))))

Length-indexed vectors

type vec a : nat -> Type =
  | Nil : vec a 0
  | Cons : hd:a -> tl:vec a n -> vec a (n + 1)

let rec append (v1:vec a n) (v2:vec a m)
  : vec a (n + m) =
  match v1 with
  | Nil -> v2
  | Cons hd tl -> Cons hd (append tl v2)

Red-Black Trees

type rbtree a : nat -> color -> Type =
| Leaf : rbnode a 1 Black
| R    : left:rbnode a h Black -> value:a -> right:rbnode a h Black -> rbnode a h Red
| B    : left:rbnode a h cl -> value:a -> right:rbnode a h cr -> rbnode a (h+1) Black

Concurrent computations indexed by separation logic specs

type m : a:Type -> p:slprop -> q:(a -> slprop) -> Type =
 | Ret: post:post_t st a -> x:a -> m st a (post x) post
 | Bind: ...
 | Act: ...
 | Frame: ...
 | Par: ...

Values and Computations

“Values” aka unconditionally total terms
Two classes of types
- Value types (t): int, list int, …
- Computation types (C): conditionally pure, divergent, stateful, …
Dependent function types of the form: x:t -> C
- F* is call-by-value
- argument can't have side-effects, so value type
Two forms of refinement types
- Refined value types: x:t{p}
- Refined computation types:
  - Stateful computations that can read and write the heap: ST t pre post
  - …

The divergence effect (Dv)

Some useful code really is not always terminating, e.g., an interpreter for a Turing complete language

let rec eval (e:exp) : Dv exp =
  match e with
  | App (Lam x e1) e2 -> eval (subst x e2 e1)
  | App e1 e2 -> eval (App (eval e1) e2)
  | Lam x e1 -> Lam x (eval e1)
  | _ -> e
(* (\x. x x) (\x. x x) *)
let main = eval (App (Lam 0 (App (Var 0) (Var 0)))
                     (Lam 0 (App (Var 0) (Var 0))))

  let rec server () =
    let x = get_request () in
    fork (handle x);
    server()

F* effect system encapsulates effectful code

Pure code cannot call potentially divergent code

Only pure code can appear in specifications

val eval : expr -> Dv expr

    type tau = e:expr{e = eval e'}
                          ^^^^^^
Expected a pure expression; got an expression ... with effect "DIV"

Sub-effecting: Tot t <: Dv t
(e.g. divergent code can include pure code)

val subst : list (var * expr) -> expr -> Tot expr
eval (subst [x, Num 0] e) : Dv expr

Verifying potentially divergent programs

(partial correctness)

Using refinement types
```
val factorial : nat -> Dv nat
```

Or the Div computation type (pre- and post- conditions)

let rec eval_closed (e:exp) : Div exp
  (requires closed e)
  (ensures fun e' -> Lam? e' /\ closed e')
= match e with
  | App e1 e2 -> let Lam e1' = eval_closed e1 in
                 below_subst_beta 0 e1' e2;
                 eval_closed (subst (sub_beta e2) e1')
  | Lam e1 -> Lam e1

Dv just an abbreviation

Dv t = Div t (requires True) (ensures (fun _ -> True))

Monadic effects in F*

type st (a:Type) = heap -> Tot (a * heap)

new_effect {
 STATE : a:Type -> Effect
 with repr = st;
      return = fun (a:Type) (x:a) (h:heap) -> x, h;
      bind = fun (a b:Type) (f:st a) (g:a -> st b) (h:heap) ->
             let z, h' = f h in g z h';
      get = fun () (h:heap) -> h,h;
      put = fun (h:heap) _ -> (),h
}

this monadic definition is the model F* uses to verify stateful code
- It is an executable model, and you can choose to run your programs in the model
But, state can be primitively implemented under the hood if you like
- for instance by C stack+heap

General approach to effectful programming

Program libraries to model effects
Derive effectful actions for primitive operations
- read, write, alloc, throw, catch, fork, join, etc.
Write programs against these models and verify them with refined computation types
Extract them to OCaml, F#, C, Wasm, … Java? with primitive effects

F*:

let incr (r:ref int) : ST unit
    (ensures fun h0 _ h1 -> modifies {r} h0 h1 /\ h1.[r] = h0.[r] + 1)
    = r := !r + 1

ML:

let incr (r:ref int) : unit = r := !r + 1

void incr (int *r) { *r = *r + 1; }

Demo

Reusable Verified Artifacts

F* as a Verification Backend

But, you need to work quite hard to tune the verifier to
- Get predictable and fast proofs
- Translate failed verifications back to the user
Encoding Java in F*, not likely to be easy
- Identify a small fragment of Java
- Or consider going the other direction: generate Java from verified F*, e.g., via Scala?

Resources to learn more about F*

https://fstar-lang.org

Online tutorial in your browser
- http://fstar-lang.org/#tutorial
Many summer/winter schools, linked online
- E.g., http://fstar-lang.org/oplss2019/index.html
Many research papers
- Start with this one https://fstar-lang.org/papers/mumon/
An F* book, but still very incomplete and drafty